|
||||||||||||||||
Weiterführende Informationen zum JPG-Format
Unter velustbehafteter Kompression versteht man nicht zwangsläufig, dass das dekodierte Bild Qualität verloren hat (was natürlich bei sehr hohen Kompressionsrate nicht ausbleibt), sondern vielmehr, dass Daten bei der Kompression verloren gehen. Die dekodierten Daten entsprechen nämlich nicht exakt den ursprünglichen Daten die kodiert wurden. Es handelt sich eigentlich um Information, die verloren geht. Um beim Dekodieren trotz dieser Informationsverluste Bilder akzeptabler Qualität rekonstruieren zu können, suchte die JPEG-Kommision nach geeigneten Hilfsmitteln.Als besonders gut geeignet erwies sich die Diskrete Kosinus Transfomation DCT. Sie spielt die zentrale Rolle im "Baseline Codec", der der kleinste gemeinsamen Nenner der verschiedene Modi ist. Der "Baseline Codec" setzt sich aus folgende Schritten zusammen:
FarbmodellDa der JPEG-Standard kein Farbmodell vorschreibt, kann das Bild im Prinzip ohne vorherige Konvertierung komprimiert werden. Es hat sich aber gezeigt, dass sich bestimmte Farbmodelle besser eignen als andere.Das menschliche Auge ist nämlich in der Lage, geringe Helligkeitsunterschiede besser zu erkennen als Farbveränderungen. Aus diesem Grund verwendet man meist sogenannte Helligkeit-Farbigkeit-Modelle, wie etwa das YUV-Modell oder das YCbCr-Modell. Während beim RGB-Farbmodell die Helligkeit und Farbe eines Bildpunktes durch seinen Anteil an Rot, Grün und Blau bestimmt wird, wird beim YUV-Modell die Helligkeit Y (Luminanz), der Farbton U und die Farbsättingung V (Chrominanz) gespeichert. Die YUV-Komponenten lassen sich leicht mit gewichteten Summen aus den RGB-Werten errechnen:
Man sieht, dass die Farben nicht zu gleichen Teilen in die Formel eingehen, was daran liegt, dass das Auge des Menschen zum Beispiel für Grün sehr empfindlich ist. Aus diesem Grund ist der Faktor der Grünkomponente bei der Berechnung von Y auch am höchsten. Mit dem gleichen Y arbeitet auch das YCbCr-Farbmodell. In den 2 Komponenten Cb und Cr werden jedoch jeweils die Abweichungen vom Grau zum Blau- bzw. Rotwert gespeichert.
Die DCT besitzt nun 64 Basisfunktion, die jeweils aus 8x8 Pixeln bestehen. Nimmt man jede dieser Funktionen als 64-stelligen Vektor, bilden diese 64 Vektoren eine Orthonormalbasis bezüglich eines Vektorraums. Wird der zu kodierende Block nach einer Basistransformation durch die DCT bezüglich der eben beschrieben Basis dargestellt, erhält man 64 Koeffizienten, die angeben, wie stark die einzelnen Basisfunktionen an dem zu kodierende Block beteiligt sind. Diese Koeffizienten heißen DCT-Koeffizienten, und werden folgendermaßen berechnet:

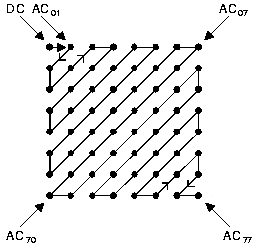
Betrachtet man die Basisfunktionen der 2-dimensionalen DCT, die eigentlich ein Produkt zweier eindimensionaler DCT ist, stellt man fest, dass sich in der linken oberen Ecke die einzige konstante Basisfunktion befindet. Der Koeffizient dieser Funktion, deren Frequenz in beiden Dimensionen Null ist, heißt DC-Koeffizient (direct-current terms), während die übrigen 63 Koeffizienten AC-Koeffienten (alternating-current terms) heißen. Bis zu diesem Zeitpunkt wurde noch keine Kompression der Daten erreicht, sie wurden lediglich für die anschließende Kompression konditioniert.
Im eigentlich verlustbehafteten Prozeß der Quantisierung werden die 64 DCT-Koeffizienten nun dividiert und das Ergebnis auf eine ganze Zahl gerundet. Die Division geschieht anhand einer Quantisierungstabelle, die die Farb- und Helligkeitsempfindlichkeit des Auges berücksichtigt. Das menschliche Auge reagiert auf niedrige Frequenzen viel empfindlicher als auf hohe. Die Koeffizienten höherer Frequenzen werden deshalb durch höhere Zahlen geteilt als die der niedrigeren. Hiermit erreicht man, dass sich der Wertebereich verkleinert. Viele Koeffizienten werden auch zu Null.
Da die Art der Quantisierung nicht fest vorgeschrieben ist, kann an dieser Stelle die Qualität des Bildes, durch die Wahl der Quantisierungstabelle mitbestimmt werden. Diese Tatsache bewirkt aber auch, dass die verwendete Quantisierungstabelle mit abgespeichert und dem Dekodierer mitgeschickt werden muss.
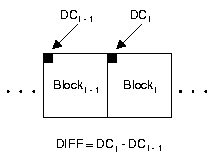
Nach der Quantisierung werden die DC- und AC Koeffizienten getrennt voneinader betrachtet.
Im letzen Kodierschritt werden dann die DCT Koeffizienten kodiert, wodurch noch eine weitere Kompression (ohne Verluste) erreicht wird. Die geschieht, indem man die charakteristische Verteilung der DCT-Basisfunktionen ausnutzt. Zur Kodierung werden Codes mit variablen Längen verwendet wie Variable-Length-Integers (VLI) und Huffmann Codes (VLC). Nun macht man sich die oben bereits beschrieben längeren Nullketten, die dann von einem von Null verschiedenen AC-Koeffizienten gefolgt werden, zu Nutzen. Anstatt nämlich jeden Koeffizenten einzeln zu speichern, wird jeder AC-Koeffizient, der nicht Null ist, in Kombination mit der Anzahl der Nullen, die ihm vorausgegangen sind, angegeben. Dies geschieht mit Hilfe von 2 Symbolen: Das erste Symbol enthält die Länge der Nullfolge und die Anzahl der Bits, die benötigt werden, um Symbol 2 darzustellen. ähnlich wird auch die Kodierung des DC-Koeffizienten, bzw. der errechneten Differenz vorgenommen. Neben einen abweichenden Symbol 1 wird auch eine andere Huffmann-Tabelle verwendet Neben der Huffmann-Codierung ist es möglich, die Koeffizienten mit arithmetischen Codes zu kodieren. Dadurch ist es möglich, eine 5-10% stärkere Komprimierung erreichen. Da die arithmetischen Codes allerdings patentiert sind, stellt sich die Frage, ob es sich für diese vergleichsweise geringen Dateneinsparungen lohnt, Gebühren zu bezahlen. Die Quantisierungstabellen und die Tabellen für die Huffmann-Codierung sind nicht fest vom JPEG-Standard vorgegeben, was einerseits eine Flexibiltät bei der Kompression bedeutet, andererseits aber auch, dass diese Tabellen immer mit dem komprimierten Bild mitgeschickt werden müssen.
Bei der Dekodierung werden alle Schritte des Kodierens in invertierter Reihenfolge rückgängig gemacht.
Nach Anwendung der inversen Diskreten Cosinus-Transformation kann das Bild jetzt rekronstruiert werden.
Dies ist also die generelle Funktionsweise des JPEG-Algorithmus, der auf der DCT basiert. Da der Standard jedoch nicht allzu genau festgelegt ist, bleibt viel Raum für verschiedene Implementationen. DCT-basierte MethodenSequentielles Kodieren Bei dieser auf DCT-basierenden Methode werden die 8x8 Blöcke von links nach rechts und Reihe für Reihe von oben nach unten gelesen. So baut sich dann auch das Bild beim Dekodieren auf.
Progressives Kodieren Diese Methode arbeitet die Blöcke in der gleichen Reihenfolge wie oben ab, wenn auch in mehreren Durchläufen. Um dies zu realisieren, muss zwischen Quantisierung und Kodierung noch ein Speicher (memory buffer) eingebaut werden. Die Koeffizienten jedes transformierten und quantisierten Blocks werden dort gespeichert und in den verschiedenen Durchläufen, je nach Wichtigkeit kodiert. So kann das Bild beim Dekodieren in schlechter Qualität aufgebaut werden. Diese Qualität verbessert sich dann in mehreren Schritten bis zum gewünschten Ergebnis.
Hierarchisches Kodieren Das hierarchische Verfahren arbeitet nach dem Prinzip des progressiven Verfahren und kodiert die Bilder in einer Pyramidenstruktur. Man verwendet es vor allem für Bilder, mit hohen Auflösungen oder in Umgebungen, die verschiedene Auflösungen darstellen können. Für Details möchte ich auf den Artikel von G.K. Wallace [1] sowie die übrige angegebene Literatur verweisen. Datenströme bei der KodierungDa bisher nur die grundlegende Funktionsweise von JPEG betrachtet wurde, werden natürlich Fragen nach Details laut, wie beispielsweise die nach Datenstrukturen.Im ersten Teil wurden bereits die Farbformate angesprochen, aber in der Erklärung der grundlegenden JPEG-Funktionsweise nicht weiter berücksichtigt. Es wurde nämlich vereinfachend angenommen, dass das Bild nur aus einer einzigen Komponente besteht. Jede Komponente besteht aus einem rechteckigen Feld von Farbwerten. Ein Farbwerte wird durch ein ganzzahligen Wert ohne Vorzeichen definiert, der in einem Bereich von [0, 2P - 1], mit einer Genauigkeit P liegt. Diese Genauigkeit muss bei allen Farbwerten aller Komponenten gleich sein und liegt beim Baseline Codec bei 8 Bit. Die i-te Komponente hat die Abtastgrößen xi und yi. Da aber verschiedene Komponenten mit verschiedenen Raten abgetastet werden können, kann es zu Komponenten mit verschiedenen Größen kommen. Diese Größen müssen nun in Einklang gebracht werden, was mit folgender Formel geschieht: Nimmt man beispielsweise ein Bild mit drei Kompenenten, dessen Größe 512 Zeilen und 512 Reihen beträgt und die Komponenten folgende Abtastraten haben:
Dann lassen sich mit X=512, Y=512, Hmax=4 und Vmax=2 folgende xi bzw. yi berechnen
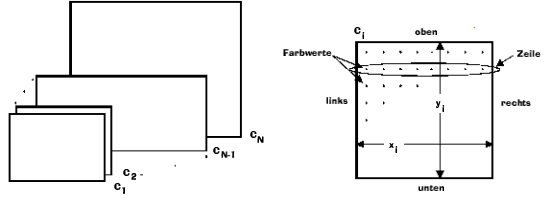
Zur Verdeutlichung der Komponenten sollen die folgenden Grafiken dienen.
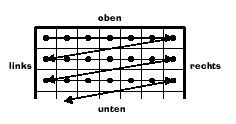
Bevor ich nun den Aufbau der Datenströme beschreibe, sollte noch der Begriff der Dateneinheit geklärt werden. Bei den auf der DCT-basierenden JPEG-Algorithmen beschreibt eine Dateneinheit einen 8x8 Block. Die Art der Kodierung der Daten des Bildes hängt im Wesentlichen davon ab, wieviele Bildkomponenten in einem Durchgang codiert werden. Hier gibt es zwei Möglichkeiten, die sogenannte "non-interleaved"- und "interleaved" - Reihenfolge "non-interleaved"- Reihenfolge In einem Durchlauf wird nur eine Komponente codiert, indem alle Dateneinheiten einer Komponenten nach unten gezeigtem Schema von links nach rechts und von oben nach unten abgearbeitet werden. Im zweiten Durchgang geschieht das Gleiche mit der nächsten Komponente. Die minimal-codierten Einheiten (Minimum coded unit: MCU), zu der Dateneinheiten zusammengefasst werden, ist bei "non-interleaved" Daten genau eine Data unit Bei der "interleaved" - Reihenfolge werden pro Durchlauf mindestens zwei Komponenten kodiert, indem jede Bildkomponente Ci in rechteckige Felder mit Hi horizonztalen und Vi vertikalen Dateneinheiten zerlegt wird.Wie groß die MCU bei dieser Reihefolge ist und wie sie sich zusammensetzt, hängt von den Abtastfaktoren der Komponenten ab. Das Prinzip sollte mit folgender Grafik deutlich werden. Wie schon öfter erwähnt, ist der JPEG-Standard sehr großzügig gehalten, um seinen Ansprüchen gerecht zu werden. Eventuelle Skepsis, dieser Standard sei wegen seiner Komplexität sehr unübersichtlich, wird dadurch aufgehoben, dass vielmehr eine Art Baukasten mit vielen Hilfsmitteln geboten werden soll, der je nach Bildbeschaffenheit, eine optimale Kodiermöglichkeit bieten soll.
Auszug aus Vortrag von Sandra Bartl (7. Februar 1999) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

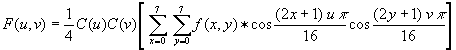
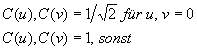


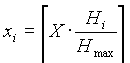
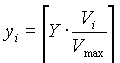
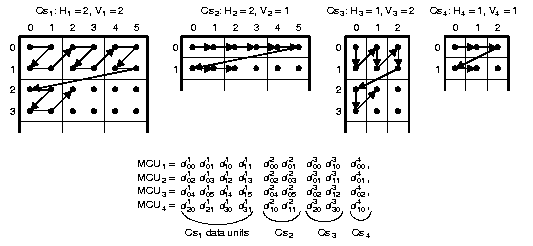 Nachdem nun immer wieder die 8x8-Blöcke erwähnt wurden, liegt die Frage nahe, was passiert, wenn nun einmal keine Vielfachen von 8 in der Horizontalen bzw. Vertikalen vorliegen. In diesem Fall werden die Reihe bzw. Spalten zu Vielfachen von 8 ergänzt und die überflüssigen Daten später wieder gelöscht.
Nachdem nun immer wieder die 8x8-Blöcke erwähnt wurden, liegt die Frage nahe, was passiert, wenn nun einmal keine Vielfachen von 8 in der Horizontalen bzw. Vertikalen vorliegen. In diesem Fall werden die Reihe bzw. Spalten zu Vielfachen von 8 ergänzt und die überflüssigen Daten später wieder gelöscht.